Researchers from the Laboratory for Dynamics of Machines and Structures (LADISK) have developed a new method for displaying magnified mode-shapes captured with a high-speed camera. The results of the study are published in the journal Mechanical Systems and Signal Processing (IF: 7,9).
The goal of motion magnification methods is to display subtle movements that are not detectable with the naked eye by processing digital video recordings. Currently, the most used motion magnification methods are based on spatial-temporal bandpass filtering of digital videos. In the field of structural dynamics, motion magnification methods are used to display and analyse the response of structures to dynamic excitation. Applying these methods to footage captured with a high-speed camera allows researchers to consider high-frequency oscillations.
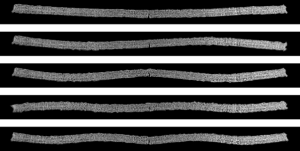
Photo: At high frequencies, structures oscillate with small amplitudes, which are often obscured by the high noise threshold characteristic of image-based displacement identification methods.
In the presented work, the authors explore the possibility of motion magnification based on experimental modal analysis. The response of the structure to dynamic excitation is measured using a simplified optical flow method based on the gradient of intensity. Combined with concurrent reference measurement with an accelerometer, a hybrid modal analysis is performed, enabling the identification of structural dynamics in areas where displacements are smaller than one pixel and obscured by noise. The identified mode-shapes of the structure represent a dense field of displacements, based on which, in the final step of the presented method, a distortion of the structure’s image is performed.
In the experimental part, using the proposed method on the example of bending oscillations of a steel beam, magnification factors of up to approximately 40,000 times were achieved. Thus, the researchers penetrated one order of magnitude deeper into the noise than existing methods allow. Moreover, the proposed approach is also numerically significantly less demanding.
